📑 [The Principles of Diffusion Models] 시리즈
CH2. Variational Perspective: From VAEs to DDPMs
들어가기에 앞서... manifold hypothesis 는 알아두면 좋을 것 같아서 링크 하나 첨부한다.
https://devs0n.tistory.com/167

VAE -> DDPM 으로 변화하는 흐름을 잘 이해하기 위해서는 일단 VAE 에 대해서 알고 있어야한다. CH2. 에서는 VAE 에서부터 시작해서 논의를 이어 나간다고 한다. 먼저 전체적인 흐름을 먼저 보면
1) vae : 데이터 -> z -> 데이터
x( 데이터 ) -> q(z|x) ( 학습된 인코더 ) -> z ( latent space ) -> p(x|z) -> x_hat ( 복원된 데이터 ) 형태이다.
우리가 part a 에서도 말했듯이. log p(x) 를 못구하니까 EBLO 아는 lower bound 를 최대화 하는 식으로 학습한다.
( 이떄 variational inference 가 핵심이다. )
(cf. https://ratsgo.github.io/generative%20model/2017/12/19/vi/ )
2) Hierarchical VAE : z 를 여러층을 쌓는다.
대략 x -> z1 -> z2 .... -> zk 이런식으로 변화한다.
복잡한 구조에 대해서 한층의 z 로 부족해서 latent 를 여러층으로 쌓아올리는 구조이다.
3) Diffusion
" Diffusion 을 매우 거대한 Hierarchical VAE 로 볼 수 있다 " 가 이번 챕터에서 가장 중요한 내용인 것 같다.
나도 막연하게 vae 를 배우고 diffusion 을 배웠을때 어떻게 이걸 표현하면 좋을까 엄청 고민했는데 다시 읽고나니 전체적인 흐름을 읽을 수 있어서 많이 명확해졌다.
디퓨전에서 latent 는
x0 (data ) -> x1 -> .... -> xt ( noise )
다음과 같이 생겼는데 , xo -> x1 ... -> xt 전체가 latent hierarchy 라고 생각하면 되는것이다. ( 단계가 굉장히 많은.. )
차이점으로
diffusion에서 인코더는 따로 학습하지 않는다. ( 디퓨전에서 인코더는 노이즈를 추가하는 fixed gaussian noise 이기 때문이다. )
마지막 문단에서 " 이 모델들은 모두 ELBO 를 최적화하는 likelihood 기반 생성모델이다" 라는 문장이 있듯이
vae , diffusion 모두 ELBO 를 최적화하는 모델이다. 이제한번 자세히 알아보도록 하겠다.
2.1 Variational Autoencoder
vae 는 복잡한 고차원 데이터 (x) 의 구조 (latent) 를 확률적으로 생성하는 모델이다.
기존 autoencoder 는 reconstruct 는 하지만 generate 하는 능력은 없다.
X -> encoder -> z - >Decoder -> x_hat
이런 형식인데 문제는 공간 z 가 아무런 구조없이 흩어져있다. ( 각 데이터 x 를 아무곳 (z) 에다 넣어두고 그냥 그 위치에서 잘 복원되기만 하면됨 -> 이러면 분포가 scatter 하고 hole 이 매우 많이 생길 것이다.따라서interpolation 하면 이상한 샘플이 나오기 쉽다.)
그래서 random z -> 의미 없는 이미지 일 뿐만 아니라 z 공간이 불연속 적이고 interpolation 도 불가능하다. 이런 문제점을 해결한게 vae 이다.
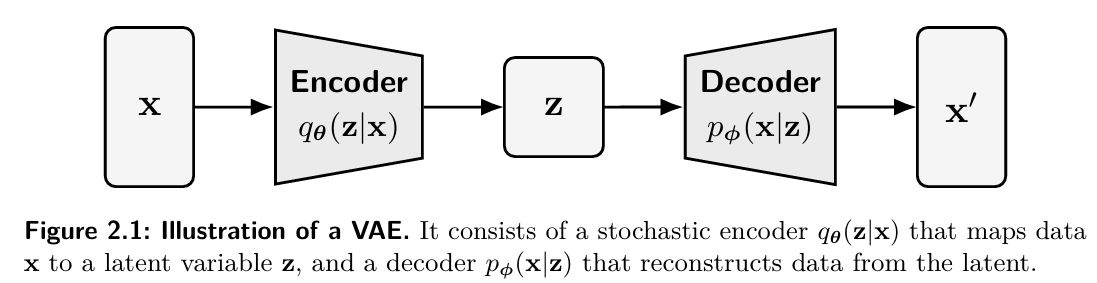
1. VAE 의 핵심 아이디어
" latent space 에 구조를 넣자 "
z 공간이 연속적이고 smooth 하게 생기도록 강제한다. 이를 위해서 latent 를 확률 변수로 선언한다.
z ~ N( 0 , I )
x ~ pϕ(x | z) ( decoder )
이렇게 되면 prior p(z) = N(0,I) 는 latent 를 압축하는 coordinate 를 제공한다.
생성형 프로세스에서는
1. 무작위로 latent z 를 뽑음 ( z~ N(0,I) )
2. z 를 decoder 에 통과시켜 이미지 생성 ( x ~ pϕ(x | z) )
z 를 표준 정규 분포에서 뽑은걸 decoder p 를 통해 x 를 생성하는 것이 목적이다.
이렇게 마무리가 되면 좋겠지만 pϕ(x) 를 계산하는 것이 너무 어렵다.

다음과 같은 꼴로 적분을 계산해야 하는데 , 이부분의 계산은 현실적으로 불가능하다. 조금 더 자세히 알아보자.
Construction of Encoder (Inference Network).
vae 에서는 x 로부터 z가 뭐였는지 알고싶을 것이다. ( 기본 가정이 데이터 x 가 latent space z 에서 나왔다고 가정했으니 )
그러면 자연스럽게 x(이미지) 가 주어졌을때, 어떤 z 가 x 를 만든 것인지 알고싶어진다. (x->z)
-> 조금 더 쉽게 이야기 하자면 우리는 이미지는 관측을 했고 , 이미지를 만든 z ( latent ) 는 뭐였지 ?
(p (z|x) ( posterior 를 알고 싶은 것이다. )
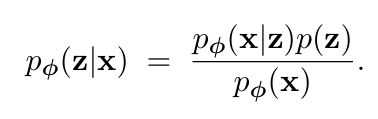
원래는 베이지안 을 통해서 해당 계산을 하고싶으나, 현실적으로 구하는 것이 불가능하다.
여기서 p(x) 가 계산이 불가능한데

1. z 가 매우 high dimension 이기 때문에 현실적으로 적분이 불가능하다.
2. p(x|z) 는 neural network 인데 계산이 매우 복잡하다.
는 수학적인 이유로 불가능하다.
( 직관적으로 이해를 해보자면 이미지 (x) 가 있고 이 이미지를 이루고 있다고 가정되는 여러가지 요소 (ex : 색 , 크기 , 구도 ,,,,, ) 등등 숨겨진 요소 (Z) 가 있다고 가정해보자. 우리는 그러면 p(z|x) 그니까 이미지를 보고나서 이런 요소가 어떤것인지 구하고 싶은 것이다.
bayes rule 계산식을 보면 , 모든 조합 (z) 를 하나씩 다 넣어보고 -> 어느 조합이 이미지(x) 를 만들 확률이 높은지를 계산하는게

아래 이 수식이다. z 가 거의 32~256 차원이면 조합수가 어마어마하게 많아질 뿐만 아니라 decoder 는 신경망이라 계산이 매우 복잡하다. 즉, 가능한 z를 하나하나 넣어보는건 너무 비효율적이된다.
--> 모든 가능한 z에 대해서, 그 z가 x를 만들어낼 확률을 다 더한 값이 커지도록 모델을 학습시키고 싶은것. )
그래서 vae 에서는 다음과 같이 해결하려고 한다.
1. 진짜 정답 분포 : p(z|x) -> 하지만 위에서 전개했듯이 계산이 불가능.
2. x->z mapping 이 반드시 필요하긴함.( 데이터를 보고 latent space 를 학습시켜야 하는건 자명하므로)
3. 그럼 p(z|x) 와 유사한 q(z|x) 를 사용하자.

다시 vae 파이프라인을 보면
x ----> [encoder] ----> z ----> [decoder] ----> x̂
다음과 같은 흐름을 가지고 있는데 encoder 는 실제 x 를 받아서 z 를 만드는 네트워크이다. 이를 이용해서 p(z|x) 가 진짜 생성모델이기는 하지만 우리는 하나의 가정 즉, encoder 에서 사용하는 q(z|x) 를 inference 역할로 보는 것이다.
다시 정리하자면 우리는 사실 디코더로 z 에서 x 를 생성하는것만 알고싶은데 , 현실적으로 이를 계산하기 어려우니 인코더를 붙여서 여기서 나온 q(z|x) 를 생성 모델로 근사시켜서 사용하기 위해 encoder 를 붙였다 라고 이해하면 되겠다. ( 실제로 vae 논문에도 그렇게 나와 있었던 것 같기도 하다. )
정리하고 다시 읽어보니 오히려 더 헷갈리는 것도 같아서 일단 짧게 정리를하면
- 나는 원래 decoder p(x|z) 만 필요함 -> 현실적인 문제로 불가능
- p(x|z) 근사한 q(z|x) 를 사용하기 위해 encoder 를 만든다.
q1. 그렇다면 왜 q(z|x) 는 확률 분포 형태여야 하나 ?
a1. 맨 처음 이야기했던 autoencoder 와 vae 가 다른 이유는
" latent space 를 확률적으로 정돈된 , smooth 한 공간으로 만드는 것 " 이다.
이를 위해서 2가지가 필요하다.
1. x 를 하나의 z 로 보내지 않고 , z의 "분포" 로 보내야함
2. latent 가 prior N ( 0 ,I ) 에 align 되도록 KL term 이 필요하다 ( 이부분은 뒤에서 더 자세히 다룬다. )
2.1.2 Training via the Evidence Lower Bound (ELBO)

ELBO 에 대한 요약은 이렇다.
원래 목표: log pϕ(x) (log-likelihood)를 최대화하고 싶다.
→ 앞에서 설명했듯이 계산이 안 된다.
→ 그래서 대신 ELBO라는 “계산 가능한 lower bound”를 만들어서 그걸 최대화한다.
→ 이 ELBO는
- 재구성 항 (reconstruction)
- 잠재 KL (latent regularization) 둘의 합으로 쪼개진다.
그리고 log pϕ(x) − ELBO = KL(q(z|x) || pϕ(z|x)) 라는 사실 때문에,
ELBO를 키운다는 건
곧
(1) log-likelihood를 키우면서,
(2) 동시에 q(z|x)가 진짜 posterior p(z|x)에 가까워지도록 만드는 것이다.

우리가 원래 최대화 하고 싶은 수식은 다음과 같다. 하지만 위에서도 이야기 했듯이 pϕ(x, z) = p(z) pϕ(x|z) 의 수식이 high dimension z 에 대해서 적분이 불가능하다
-> 자연스럽게 log p(x) 의 최대화가 불가능해진다.
그래서 직접 계산을 못하면 계산 가능한 lower bound 를 만들자는 것이 eblo 의 가장 큰 목적.
<수식전개>

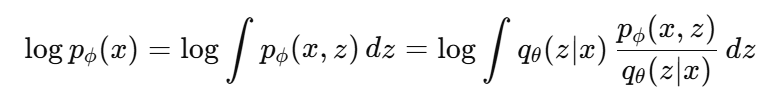
- 기존 수식에 분자/분모에 qθ(z|x)를 곱했다가 나눈다.

그러면 결국 log E[...] 꼴로 변형을 할 수 있다.
-> 그리고 JENSEN 부등식을 사용한다. ( log E[Y] > E[logY] )
그리고 수식을 다음과 같이 정의한다 ( ELBO 의 정의 )

<ELBO>
ELBO 수식에 대해서 조금 더 풀어보자.

- pϕ(x,z) = p(z)pϕ(x|z)
- 따라서 log pϕ(x,z) = log pϕ(x|z) + log p(z)
- 이렇게하면 3개 항으로 쪼갤 수 있다.

여기서 두번쨰와 세번째 항을 합치면 KL 이 나온다.
( kl(p||q ) -> sum ( p(x) log ( p(x) / q(x) ) ) == E[log(q) / log(p) ] ) 정의대로 쓰면 이렇게 정리가된다.




따라서 최종 형태는 다음과 같다. ( 책의 수식과 동일해짐 )
이렇게 구성하면 계산이 매우 쉬워진다.
(1) Reconstruction term : z 로부터 얼마나 x 를 잘 복원하는지 ?
-> 중요한점 :
만약에 reconstruction term 으로만 최적화 하면 문제가 생기는데 이 문제는 바로 "Memorization" 이다.
이 항만 있으면 encoder 가 q(z|x) 를 그냥 아무렇게나 인코딩해도 decoder 는 그냥 p(x|z) 를 통해서 그냥 x 를 복사만해도 loss 가 작아지게 되는데 이렇게 되면 latent space 에 구조가 없어지게 된다.
-> autoencoder 를 생성형 모델로 쓸수 없는 이유이기도 하다.
-> vae 에서는 kl regularization 을 반드시 넣어야 한다. ( vq-vqe 에서도 이런 형식으로 구성된다. )
(2) Latent Regularization (KL Divergence) : q(z|x) 가 prior (z) 에 얼마나 가까운지 ?
q(z|x) = N(0,I) 와 유사해지도록 강제하는 Regularization 이다.
원문 : This regularization shapes the latent space into a smooth and continuous structure, enabling meaningful generation by ensuring that samples drawn from the prior can be reliably decoded. This regularization shapes the latent space into a smooth and continuous structure, enabling meaningful generation by ensuring that samples drawn from the prior can be reliably decoded.
여기엔 먼저 2가지 가정이 필요하다.
1. p(z) 는 정규 분포로 가정한다.
- 이렇게 prior 을 단순한 gaussian 으로 고정해야 KL 계산이 잘 되고 , latent space 가 잘 정돈될 뿐만 아니라 샘플링이 쉽다.
- 여기서 log p(z) ( 샘플 z 를 정규분포 p 에 넣은 값. )
2. Encoder q(z|x) 도 tractable 한 분포여야 함.

- encoder 가 정규분포 형태를 출력한다고 가정한다.
- 이런 가정이 있어야 KL(q||p) 를 closed form 으로 계산이 가능함
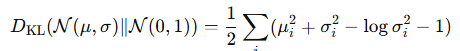
( 자세한건 cf. https://di-bigdata-study.tistory.com/5
그럼 무슨 역할을 하나 ?
1)
latent space 를 N(0,I) 주변으로 정렬 시킬 수 있다.
모든 x 를 encoding 한 q(z|x) 가 gaussian prior 주변에 모이게 된다.
encoder 가 만든 분포 ( q(z|x) ) 가 prior p(z) 에서 멀어질 수록 패널티가 커지니까 둘이 분포가 비슷해짐.
자연스럽게 q(z|x) = N(0,I) 의 분포와 비슷해짐. ( 수식을 보면 Mu 은 0으로 가고 , sigma 는 1로 가야 가장 값이 작아진다. )
따라서 latent space 를 매끄러운 구조를 만든다. ( smooth + continuous )
2)
앞에서 설명한 memorization를 방지할 수 있다.
q(z|x) 의 variance 가 0 에 가까우면 사실상 latent space 가 데이터별로 멀리 흩어져있는 모양일텐데
이러면 KL term 이 0으로 가면 loss 가 사실상 무한대로 커진다.
따라서 너무 샤프한 인코딩이 금지된다.
( 추가 : memorization 은 결국 데이터별로 멀리 흩어져서 해당 데이터만 외우는 latent space 를 가질것이지만 , 우리는 그러지않고 너무 데이터를 멀리 ( var ) 두지 않기 때문인 것으로 이해하면 쉽다. )
Information-Theoretic View: ELBO as a Divergence Bound.
ELBO 를 정보이론 - 분포 관점에서 어떻게 해석하는 지에 대한 섹션이다.
이쯤에서 한번 다시 remind ( with gpt )



결국 MLE 니까 , 모델 분포 가 데이터 분포 p_data(x)를 얼마나 잘 근사하는지를 나타내는 것이다.
하지만 p_phi(x) 가 KL 도 직접 계산하기 힘들기 때문에 -> ELBO 를 사용한다.

-----------------------------------------------------------------------------------------------------------------------------------------------------------------
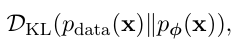
다시 책의 내용으로 돌아가 보자면 , 위의 식을 MIN 하는 것은 결국
" 모델분포 P_phi(x) 가 데이터 분포 p_data(x) 를 얼마나 잘 근사하는가 "
를 나타내는 error 이다. ( 위 식을 최소화 하는게 원래 목적이였지만 )
하지만 위에서 설명했듯이 P_phi(x) 가 구하기 힘들어서 이 KL 도 직접 계산하기 힘들다. -> 따라서 ELBO 를 사용한다.
책에서 두 joint 에 대해서 이야기한다

generative joint 는 prior p(z) = N(0,I) / p_phi(x|z) 는 vae decoder
inference joint 는 데이터 + encoder 엮어서 ( p_data(x) ) / (q(z|x) )
( 쉽게이야기하면 generatvie joint = decoder 에서 생성하는거 / inference joint = 인코더에서 z 추론하는.. )
여기서
- qθ(x,z)는 진짜 데이터 p_data(x)에
그 데이터에 대한 추론된 latent qθ(z∣x)를 붙인 joint. - pϕ(x,z)는 prior + decoder로 정의되는 모델의 joint.
이 둘의 차이를 joint KL로 비교하겠다는 게 출발점이다.
" chain rule for KL divergence "

직관적으로 이해를 해보자면
(좌측 marginal kl) : 겉으로 보이는 x 분포끼리만 비교
(우측 joint kl) : (x,z) joint 까지 비교하는 KL 은 x 뿐만아니라 x와 연결된 z 까지 포함해서 더 하드하게 비교함.
--> 이걸 정보 이론으로 이해를 해보면
joint KL 이 marginal KL 보다 크다
즉, 정보가 많으면 -> mismatch 를 더 많이 잡아낸다.
이 말을 좀 풀어서 써보면
우리 관측 가능 데이터 : x ( 이미지 )
latent : z ( 잠재 코드 )
두가지 평가 방법이 존재한다
1. 겉모습만 평가하기 ( marginal KL )
-> 이미지 x 자체의 분포만 맞는지 본다
-> 그래서 z 인자가 없는 것이고.
2. 겉 + 속 ( joint KL )
-> 이미지 x 의 본포도 보고 각 이미지 x 에 대해서 어떤 z 가 붙는지 본다
so -> D_kl ( q (x,z ) | p (x,z) )
2.
직관적으로 왜 joint 가 항상 크거나 같냐면
joint kl 은 정보를 더 많이 비교한 인자이다 ( 말하자면 문제 답 + 풀이과정을 본 경우이고 )
marginal kl 은 답만 본 경우이다.
당연히 답만 본 경우에 깎이는 점수가 덜하지 않겠는가 ?? -> 그렇다는건 loss 가 더 작다는 의미가 된다 ! ( 에러를 더 잡아냄)
따라서 joint kl 이 직관적으로 항상 더 크거나 같을 수 밖에 없다.
3.
정보가 많으면 -> mismatch 를 더 잘 잡는다.
이 역시 꽤나 직관적으로 당연한데,
marginal 같은 경우 ( x 만 볼때 ) 결국 답만 보는 경우이지만
joint kl 의 경우 ( x + latent z 를 보니까 ) 더 정보가 많을 것이다. 또 latent z 같은 경우는 x 를 일종의 추상화해서 압축시켜 둔 부분이라고 생각했을때 라고 생각해본다면 더 class 를 세밀하게 조절할 수 있는 부분이 많을것이다.
따라서 mismatch 를 잡기 더 쉽다. !
4.
total error bound 인 이유
사실 우리는 DKL(pdata(x)∥pϕ(x)) 를 줄이고 싶은데 이게 어려우니 DKL(qθ(x,z)∥pϕ(x,z)) (joint KL) 을 다루는 것이다.
joint KL 수식을 보면 모델링에러 + 추론 에러가 합쳐서 들어가 있다
둘이 합쳐서 들어가 있으니 TOTAL ERROR 로 보는듯.
또,
모델링에러 ( 원래 알고싶은값 ) <= JOINT KL (TOTAL ERROR )
이니까 joint KL 은 모델링 에러에 대한 upperbound 이다.
( 이걸 kl 의 chain rule 이라고 부른다고 한다. )
수식 전개를 해보면.

True modeling error :
- 모델의 marginal pϕ(x)가 진짜 데이터 분포를 얼마나 잘/못 맞추는지 ( 우리가 원래 구하고자 했던 값 )
- 이미지 x 자체의 분포만 맞는지 본다 <-> ( joint kl 은 이미지 분포 x 도 보고 / 이미지 x 에 대해서 어떤 z 가 붙는지 같이 본다. )
inference error :
- 진짜 posterior pϕ(z∣x)와 encoder가 근사한 qθ(z∣x)사이의 mismatch 평균 ( posterior p 와 encoder 가 근사한 값 q 사이의 평균 )
이때 inference error 는 항상 0보다 크니까 결국

다음과 같은 수식이 만족되는 것이다
( joint KL = modelling error + inference error )
-> joint KL 이 크다는건
1. 모델 자체에 오류가 있거나
2. encoder 추론이 별로여서 posterior 를 잘 못따라 가거나
둘중 하나 혹은 두개라는 의미를 가지게 된다.
ELBO and inference error
결국 위의 수식을 정리하면 다음과 같이 정리할 수 있다.
( cf.


이 식의 뜻은 즉
"log likelihood 랑 ELBO 사이의 gap 이 posterior 를 얼마나 잘 근사했는지 ( inference error ) 랑 정확히 같다 "
log p_phi(x) : 우리가 정말 최적화 하고싶은 likelihood
L_elbo : 우리가 실제로 최적화 할 수 있는 것
둘의 차이가 D_KL = ( encoder posterior 근사 오차 )
그래서 결국 elbo 를 최대화 한다는건
1. 모델링 에러를 줄이는 방향으로 학습하면서
2. inference error 도 줄이는 것이다.
ELBO 가 logp(x) 에 가까워 질수록 -> q(z|x) 가 진짜 posterior p(z|x) 에 가까워 지고 있다는 의미이다.
2.1.3 Gaussian VAE

원문 그대로라 설명할게 많지는 않다
(1) 인코더 qθ(z∣x)
- latent z 를 도입해서 데이터를 설명하려고 함
- x ( 이미지 ) -> z 에 대한 분포를 뱉는다.
- 다만 여기서 인코더는 하나의 벡터가 아니라 정규분포 ( 평균 + 분산 ) 을 내보낸다는점.
(2) 디코더 p(x|z)

- latent -> data 공간으로 가는 디코더
- 분산은 고정된 스칼라 + isotropic 가우시안 ( 즉 , 디코더는 평균만 학습하고 , 분산은 그냥 상수로 고정함. )
Reconstrction term 이 MSE 가 되는 이유 ?

위에서 살펴본 Reconstrcution term 이다. pϕ(x∣z)가 가우시안이라고 했으니 로그를 풀면

다음과 같이 되는데 C 는 상수니까 무시 ( 변수 phi 랑 theta 랑 관련없 )
so ,

따라서 MSE 꼴이 된다.
결국 EBLO 를 최대화 하려면 -> Reconstruction term 을 최대화 해야하니까 -> (위가 마이너스 mse 이므로 ) -> 위 항을 최소화 하는 것과 같다고 볼 수 있다.
( 의미적으로는 디코더가 x 를 잘 재구성하도록 mse recontrctuion loss 를 최소화 하는거랑 같다고 이해하면 되겠다. )

따라서 ELBO 수식을 다시 정리하면 다음과 같다.
1 : mse
2 : KL
( KL 은 앞에서도 서술 했지만 q 와 p 둘다 가우시안 이니까 closed-form 으로 계산하기 편하다. )
<정리>
VAE loss를 직관적으로 보면:
- 재구성 항:
- 오토인코더처럼 x를 잘 복원하도록 MSE를 줄임.
- z에서 다시 x로 갈 때 정보 손실이 적게.
- KL 정규화 항:
- 각 x에 대해 나오는 qθ(z∣x)가 prior N(0,I)와 너무 다르지 않게 묶어줌.
- 그래서 “latent space 전체가 부드럽고 연속적”이 되고,
- 무작위로 z∼N(0,I)샘플 뽑아서 디코더에 넣어도 그럴듯한 x가 나오게 됨.
요약하면:
VAE 학습 = “재구성 MSE를 줄이면서, latent 분포를 표준정규에 가깝게 만드는 최적화”
2.1.4 Drawbacks of Standard VAE
2.1.5 (Optional) From Standard VAE to Hierarchical VAEs

Hierarchical Variational Autoencoders (HVAEs) 는 latent 를 단계적으로 쌓은 모델이다. 위쪽 latent 가 전반적인 구조 ( 거친정보 ) 를 가지고 아래쪽 latent 가 점점 더디테일을 담당하는 형식이다.( 벌써 디퓨전과 모델이 매우 비슷하게 생겼다) 조금 더 자세히 서술해 보겠다.
HVAE vs VAE
기존 vae
- latent 가 한개

HAVE
- latent 를 여러 층으로 쌓음 ( z1 ,,,, zl )
- 의미를 이렇게 파악하면 편하다
-> z_L : 제일 위 , 가장 추상적인 정보 ( 전체 느낌 )
-> z_1 : 가장 아래 , 디테일에 가까운 정보
-> x 실제 이미지
HVAE's Modeling
(Decoding)

HVAE 에서 이미지를 생성하는 수식은 다음과 같다. 복잡해보이지만 매우 단순한데 ( 위쪽의 그림을 보면 바로 이해가 된다 )
맨위 Latent 를 샘플링한다 => z_L ~ p(z_L)
그 다음 위에서부터 아래로 차례대로 latent 를 생성한다

그리고 마지막으로 실제 데이터 생성을 하면 ( p(x|z1) ) 끝이다. ( 매우 직관적이다. )
coarse -> fine 방향으로 정보를 점점 풀어내면서 x 를 만든다.
(top-down)
(Encoding)
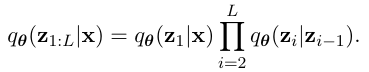
인코딩은 반대로 x 에서 시작해 z 를 추출한다음 단계를 올라가 z_l 까지 도달한다.
( bottom-up )
Observation 2.1.1
레이어를 여러 층 쌓으면, 데이터 생성을 거칠게 시작해서 점점 디테일을 추가하는 방식으로 만들 수 있다.
이렇게 구성하면
1. 고차원 복잡한 구조를 나누어서 처리할 수있다
- 이미지 전체 구조 / 로컬 을 같은 z 에 넣으려면 vae 로는 표현력이 부족할 수 있음
2. Neural net 과 아이디어가 맞음
- 우리가 기존에도 어떤 복잡한 경계를 표현하기 위해서 네트워크를 깊게 쌓았는데 vae 도 마찬가지로 latent 공간 자체를 깊게 만들었다고 생각하면 된다. ( 꽤나 놀라운 직관인거같다 )
이런 아이디어가 결국 score-base / diffusion 모델에서 이런 coarse to fine ( or multi scale ) 구조가 많이 나오게 되는 시초이다.ㅣ
HVAE 의 EBLO 유도

( 수식은 머리가 살짝 아프니 잠깐 건너 띄겠다 )
Why Deeper Networks in a Flat VAE are Not Enough.
HVAE는 latent 공간을 깊게 만든 거라고 볼 수 있다 → 그렇다면 encoder/decoder만 깊게 만들면 안 되나? → 왜 굳이 z를 여러 층으로 쪼개서 쓰는가? 라는 의문으로 이어질 수 있다. ( 나도 그랬고 )
어차피 깊게 만드는 게 목적이라면, 굳이 z1,…,zL를 도입할 필요 없이 encoder와 decoder 네트워크만 깊게 만들면 되는 것 아닐까? 라는 의문이 생긴다. 본 논문에서는 단순히 encoder / decoder 를 깊게 만든느 것과 latent 계층 자체를 도입하는게 본질적으로 다르다고 설명한다.
1. variational family 가 너무 단순하다.
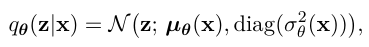
기존 vae 에서 encoder 는 보통 이렇게 두는데 아무리 encoder 네트워크(µ, σ를 출력하는 NN)를 깊게 만들어도
a. 분포의 형태 자체는 " 대각 공분산 가진 하나의 가우시안 " 에서 안벗어나고
b. 얼마나 복잡한 함수를 쓰든 결국 한 덩어리로 근사하게 된다.
( 마치 복잡한 함수를 만드려면 activate function 을 둬야 하듯이 .. )
하지만 진짜 posterior P_(z|x) 는 보통 Multi-peaked 일 수있다.
하지만 우리가 쓰는 encoder q(z|x) 는 하나의 가우시안이라 여러 피크모양인 p(z|x) 를 정확히 따라갈 수 가 없다.
즉, 네트워크를 아무리 깊게 사용해도 M , var 만 더 잘 추정하게 할 뿐이지 분포의 family 자체는 안바꾼다.
2. 그래서 Hierarchy 는 기존 방식과 무엇이 다른가 ?

1. Reconstruction loss
E[logp (x|z)] -> 여전히 얼마나 z1 로 x 를 잘 재구성 하느냐 ?
2. KL
KL divergence 쪽을 확인해보면 각 레벨별로 1:1 로 KL 로 묶여서 서로 맞추도록 학습한다. ( 수식을 풀어보자면.. )

이렇게 되면 각 inference conditional 이 자신의 top-down 이랑 짝과 aligned 되도록 KL 층이 나눠진다.
이렇게 되면
1. 정보 패널티가 층별로 분산되고
2. 학습 신호가 local 하게 전달된다. ( 각 레벨에서 자기 위/아래로만 맞추면 됨 )
그래서 이런 효과는 encoder/decoder 를 깊게 쌓는것으로는 얻을 수 없고
latent 변수들의 그래프 구조를 바꿔야지만 얻을 수 있다.
하지만 아직 한계가 존재하는데
1. joint optimize 문제
- 최적화 하기 힘들다.
2. gradient 가 깊은 latent 까지 약하게 도달한다. ( gradient vanshing 처럼.. )
3. conditionals 가 너무 강력하면 위 레벨이 죽는다. (조건 분포가 너무 expressive 하면 낮은 레벨에서 다 해결해버리니까 위에 레벨에서 할 게 없다. )
그래서 이런 HVAE 가 어떻게 Diffusion 으로 이어지는지 맛보기로 살펴보자면
1. HVAE 의 coarse -> fine 아이디어는 챙용
2. 하지만 posterior 도 같이 학습해야해서 불안정하다.
Diffusion 은
1. enoding 을 고정해버린다 -> encoding 은 noise 과정으로 통일
2. 학습은 오로지 reverse generative 과정만 한다. -> ( 그래서 posterior collapse 문제와 같은 학습 불안정성에서 많이 자유롭다 )
3. 그럼에도 불구하고 progressive , multi-step (HAVE 스타일 )은 유지를 한다.
내용이 매우 길어 졌기 때문에 글을 하나 더 작성해서 이후에 DDPM 부분을 풀어나가볼까 한다.
VAE 를 깊게 배우고 나서는 전반적으로 어떤 느낌으로 latent 를 다루는지 감을 익혔고 , HVAE 를 통해서 이 latent 를 쌓는다는게 어떤 의미인지 매우 명확하게 알게 되었다.
이를 바탕으로 DDPM 을 이해해보자.
cf. vae 에 대한 유튜브 영상
'Paper' 카테고리의 다른 글
| Why Diffusion Models Don’t Memorize 발표자료 및 의문해결.. (0) | 2025.12.09 |
|---|---|
| TRELLIS 발표자료 (0) | 2025.11.26 |
| [The Principles of Diffusion Models] ( Part A ) (0) | 2025.11.03 |
| DINO v3 발표자료 (0) | 2025.08.30 |
| VGGT 발표자료 (0) | 2025.08.16 |
