4DGS 프로젝트를 하기에 앞서서 먼저 Hex plane 에 대해서 더 이해를 해야될 것 같아서 정리한다.
먼저 간단하게 정리하면
4D공간 ( xyz + time t ) 에서 featrue field D(x,y,z,t) 를 6개의 2D feature plane(XY, XZ, YZ, XT, YT, ZT) 으로 나눠서 저장하고 , 4D 에서 점을 물어보면 ( 그니까 time + space ) 를 물어보면 해당 점을 각 plane 에 투영해서 샘플링 --> 결합 해서 그점의 feature 를 빠르게 복원하는 형식이다.
Plane 은 총 6개인데
(x,y,z,t) 에서 두 축을 고르면 2D plane 이다.
- 공간-공간: XY, XZ, YZ
- 공간-시간: XT, YT, ZT
으로 구성된다.
HexPlane 이 단순히 6개에서 feature 뽑고 concat 하는게 아니라 (공간 plane) x ( 공간-시간 plane) 을 elemtewise product 으로 묶어서 4D 상호작용 만들고 선형결합해서 feature 로 출력한다.
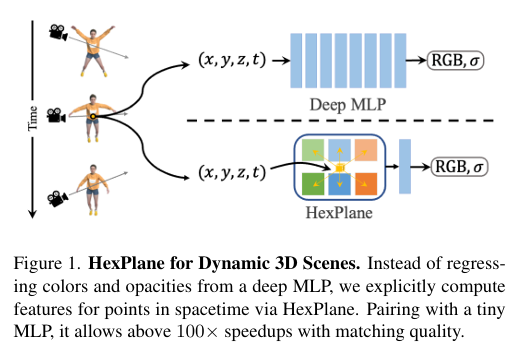
- 만약에 (XY) 만쓰면 시간에 무관한 정보가 들어가고
- (ZT) 는 시간이 포함된 Plane 이 움직임/변화를 담당하고
- 둘을 곱하면 어떤 xy 위치에서 , 시간/깊이(zt) 에 따라 달라지는지 알 수 있는 결합효과가 생긴다.

그래서 위와 같이 둘 (XY - ZT ) 을 결합해서 사용한다.
이때 왜 xy - zt 를 결합(페어링) 하는지 의문일 수 있는데 , 일단 한 곱 안에 x,y,z,t 가 모두 들어가야한다.
그리고 HexPlane가 쓰는 3개 곱은:
- (XY)×(ZT) → (x,y)와 (z,t)
- (XZ)×(YT) → (x,z)와 (y,t)
- (YZ)×(XT) → (y,z)와 (x,t)
각 항이 4개 변수 전부를 포함하고, 동시에 서로 다른 방식으로 얽힘을 잡을 수 있습니다.
- XT는 “x 방향 움직임 vs 시간” 상관을 잡기 좋고
- YT는 “y 방향 움직임 vs 시간”
- ZT는 “깊이/변형 vs 시간”
- XY/XZ/YZ는 각각 공간 구조를 잡음
그래서 이 세 항을 더하면
- 시간에 따른 이동 ( Translation )
- 시간에 따른 형태 변화 ( deformation )
- 공간 구조 기반 제약
이 3가지를 다른 관점에서 커버 가능하다고 합니다.
HexPlane 은 결국 4D field 를 low-rank 의 곱의 합으로 근사할 수 있게 된 것이다.

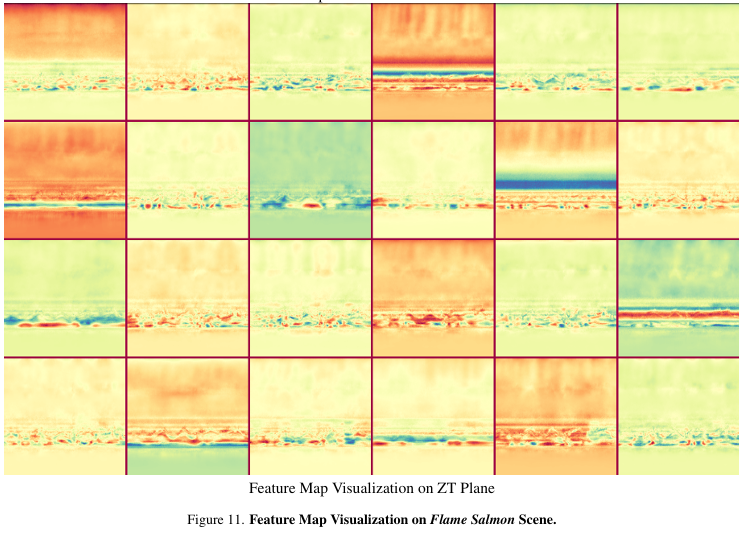
좀더 직관적으로 확인하고 싶어서 논문에서 가지고 왔습니다 ( 없으면 실험하려고 했는데 다행이네요 )
1. XY Plane 에 무엇이 들어가 있는가 ?
XY Plane 에는 "(x,y) 위치에 필요한 latent vector " 가 들어간다.
밀도랑 rgb 예측하기 위해 학습되는 latent 입니다.
그래서 조금 헷갈렸던게 왜 움직이는데 xy 는 고정인가 ? 고민을 좀 했었는데
xy 에는 시간축이 없어서 " 모든 시간에 공유되는 basis / 공간 구조 힌트" 역할을 하게 됩니다.
그래서
- xy 는 좀 폭넓게 ? 그니까 시간에 따라 덜 바뀌거나 혹은 공통의 패턴을 담을 확률이 높습니다.
- 시간 변화는 이제 다른 축이 담는거죠
그래서 xy plane 은 좀 static 을 담는다 ? 아니면 학습 과정에서 이런 역할분담이 자연스럽게 생긴다 ? 정도로 이해하면 될 것 같습니다.
cf. 4dgs 에서 좀 역동적인 동작이 어려운 이유가 여기 있을 수도 있겠네요
이거 관련해서 좀 더 리서치를 잠깐 해봤는데 ( context 가 좀 섞여서 4dgs - hexaplane 이 조금 잘못 섞여서 리서치한것 같다 )
일단
" 다만 “XY plane이 시간축이 없어서 static이라서”가 원인이라기보단, **(HexPlane/K-Planes 계열의) plane factorization 자체가 갖는 ‘저랭크(low-rank) 가정’**이 강한 동작(복잡한 non-rigid, 빠른 motion, topology change 등)에서 병목이 되는 경우가 많습니다. 그리고 여러 4DGS(=dynamic Gaussian splatting) 방법들이 효율 때문에 비슷한 ‘저랭크/기저 공유’ 형태의 motion parameterization을 쓰기 때문에, 질문하신 직관이 꽤 맞닿아 있어요 "
라고 하네요 좀 더 꼬리질문으로 들어가 봤습니다.
1. 일단 low rank 가정이 역동적인 동작에 불리할 수 있다.
일단 부드러운 움직이면 low rank 도 잘맞느는데
동작이 복잡해지면 rank 가 커져야한다. rank 가 부족하면 결국 잘 안된다.
( Spacetime Gaussian Feature Splatting for Real-Time Dynamic View Synthesis )
- Grid like 표현 방식이 장면의 구조나 움직임에 유연하게 적응하지 못하고 디테일이 부족하다.
- 그래서 해다,ㅇ 논문에서는 점들이 직접 움직이는 방식으로 확장해서 해결책 제시
-> 3dgs 에서 temporal opactiy 랑 polynomial 기반 움직임 회전 추가
(가우시안 자체가 움직이는 것 )
2. 그래서 4DGS 에서도 비슷한 이유로 나타는 건가 ?
< Deformable 3D Gaussians for High-Fidelity Monocular Dynamic Scene Reconstruction >
일단 위 논문에서는
- Canonical space + deformation field 개념 도입해서 해결 ( 그니까 Plane 을 나눈 부류가 아님 )
( Canonical space )
- 기본형태인 3DGS 세트 정의
(Deformation Field )
- 시간 t 가 주어졌을떄 공간에 있는 가우시안들이 어떻게 움직이고 변형되어야 하는지 계싼하는 MLP

관련 연구들
- Spacetime Gaussian Feature Splatting (CVPR 2024)
- HexPlane 같은 grid/plane factorization이 동적 구조에 잘 적응 못 해 디테일을 방해할 수 있다고 한계를 언급.
- SC-GS (CVPR 2024)
- 동적 장면에서 motion을 **sparse control points(기저)**로 두고, “동작이 compact subspace로 표현 가능”하다는 관찰을 사용.
- 동시에 low-rank assumption 때문에 high-rank dynamic scenes에서 underperform 가능함을 관련연구 문맥에서 언급.
- MotionGS (NeurIPS 2024)
- 기존 동적 Gaussian 계열이 명시적 motion 제약이 부족해 최적화가 어렵고 성능 저하가 난다고 지적하고, flow 기반 motion prior로 보강.
- 4D Gaussian Splatting (CVPR 2024)
- per-frame 3DGS 대신 4D를 통으로 다루는 방향.
- CoDa-4DGS (ICCV 2025)
- “복잡하고 highly dynamic”한 환경(자율주행)을 겨냥해 context + temporal deformation awareness로 보강.
2. ZT Plane
마찬가지로 grid 형태의 latent feature 가 들어갑니다.
아마도 이쪽은 시간에 따른 변화를 담당하는 축 일 것입니다. ( 학습되면서 자연스럽게 .. )
ZT 는 그러면 z 축 위치 별로 시간이 바뀌면서 어떻게 장면이 달라지는지에 대한 느낌일 것이구요
그래서 위 그림을 보면
xy : 육안으로 봐도 좀 그럴듯한 feature 모양이라면
zt : 띠 모양 형태로 시간에 따라서 위치가 이동하는 ( 시간축에서 z 의 이동 . )
< Gating >
결국 위에서 봤듯이

이런식으로 (x,y) - (z,t ) 를 곱하게 되는 형태가 된다.
만약에 같은 (x,y) 라도 , f(z,t) 가 바뀌면 결과값이 달라지는데
if f(z,t) = 0 -> 결과값도 0
즉 ZT 가 이시간 , 이 Z 축에서는 이 채널의 ON/OFF 를 적용하는 효과를 가지게 된다.
( 미분을 잠깐 생각해보면 쉽다. )
그래서 좀 더 쉽게 이야기 해보면
지금 시간 t 에서 Z 가 이 위치일때 , XY ( 단면 ) 을 키자 . ( 공간 X 위치 ) 를 자연스럽게 표현하게 된다.
< 그러면 4DGS 에서는 ? >
HexPlane ( field )
- 물어보는 방식: (x,y,z,t) 좌표를 query → σ,rgb를 예측 → ray marching/volume rendering
- 핵심 자원: 필드 파라미터(plane/MLP)
4DGS
- 그리는 방식: Gaussian들을 화면에 투영(splat) → alpha compositing
- 핵심 자원: Gaussians(중심/공분산/opacity/color) + “시간에 따른 변화 모델”
이라고 합니다.

결론적으로 output 값이 좀 다른데
위치변화 , 회전변화 , 스케일 변화 이걸 합쳐서 변형된 Gaussian 을 만듭니다.
참고로 HexPlane 방법말고 deformation 방법도 4dgs 에서 주로 쓰이고는 합니다 ( 2가지 모두 자주 사용 )
deformation 은 HexPlane 보다는 연산량이 많지만 보다 더 다이나믹한 움직임을 표현할때 자주 쓰이는 것 같아요
'ai' 카테고리의 다른 글
| [The Principles of Diffusion Models] 이해하기 - CH 3. Score-Based Perspective: From EBMs to NCSN ( 작성중 ) (1) | 2026.01.03 |
|---|---|
| latent variable Models 에 대한 개념 정리 및 생각 (0) | 2025.11.19 |
| [Vision Transformer] implement(구현) (0) | 2024.10.02 |
| Transformer 구현 (0) | 2024.08.11 |
| [논문]Chain-of-Thought Prompt Distillation for Multimodal Named Entity Recognition and Multimodal Relation Extraction (0) | 2024.05.04 |